排序算法
1 冒泡排序
void bubblesort(vector<int> &nums) {
for (int i = 0; i < nums.size(); ++i) {
for (int j = 0; j < nums.size() - 1 - i; ++j) {
if (nums[j] > nums[j + 1]) {
swap(nums[j], nums[j + 1]);
}
}
}
}
2 选择排序
void selectsort(vector<int> &nums) {
for (int i = 0; i < nums.size() - 1; ++i) {
int min_index = i;
for (int j = i + 1; j < nums.size(); ++j) {
if (nums[j] < nums[min_index]) {
min_index = j;
}
}
if (min_index != i) {
swap(nums[min_index], nums[i]);
}
}
}
3 插入排序
void insertsort(vector<int> &num) {
for (int i = 1; i < num.size(); i++) {
int insert_num = num[i], j;
for (j = i - 1; j >= 0; j--) {
if (num[j] > insert_num)
num[j + 1] = num[j];
else
break;
}
num[j + 1] = insert_num;
}
}
4 快速排序
int partition(vector<int> &arr, int low, int high) {
int pivot = arr[high];
int i = (low - 1);
for (int j = low; j < high; j++) {
if (arr[j] <= pivot) {
i++;
swap(arr[j], arr[i]);
}
}
swap(arr[i + 1], arr[high]);
return (i + 1);
}
void quicksort(vector<int> &arr, int low, int high) {
if (low < high) {
int p = partition(arr, low, high);
quicksort(arr, low, p - 1);
quicksort(arr, p + 1, high);
}
}
void quicksort(vector<int> &v,int start,int end) {//快速排序
if (start < end) {
int base=v[start];//定下基值
int low = start;//这里叫低指针好了(设置一个变量来充当指针的作用)
int heigh =end+1;//那这里叫高指针吧
while (low<high) {
while (low < end && v[++low] <= base);//从左往右找到数组中第一个比base大的值为止
while (heigh > start && v[--heigh] >= base);//从右往左找到数组中第一个比base小的值为止
if (low < heigh) {
swap(v[low], v[heigh]);//交换
}
}
swap(v[start], v[heigh]);//确定了base最后所在的位置
quicksort(v,start,heigh-1);//分而治之的思想进行递归调用,不断的确定每个base排序后最后的所在位置
quicksort(v,heigh+1,end);
}
}
5 堆排序
void heapify(vector<int> &nums, int n, int i) {
if (i >= n) {
return;
}
int c1 = 2 * i + 1; //子节点 c1 c2
int c2 = 2 * i + 2;
int max = i; // 父节点 max
if (c1 < n && nums[c1] > nums[max]) {
max = c1;
}
if (c2 < n && nums[c2] > nums[max]) {
max = c2;
}
if (max != i) {
swap(nums[max], nums[i]);
heapify(nums, n, max);
}
}
void build_heap(vector<int> &nums, int n) {
int last_node = n - 1;
int parent = (last_node - 1) / 2;
for (int i = parent; i >= 0; --i) {
heapify(nums, n, i);
}
}
void heap_sort(vector<int> &nums, int n) {
build_heap(nums, n);
for (int i = n - 1; i >= 0; i--) {
swap(nums[i], nums[0]);
heapify(nums, i, 0);
}
}
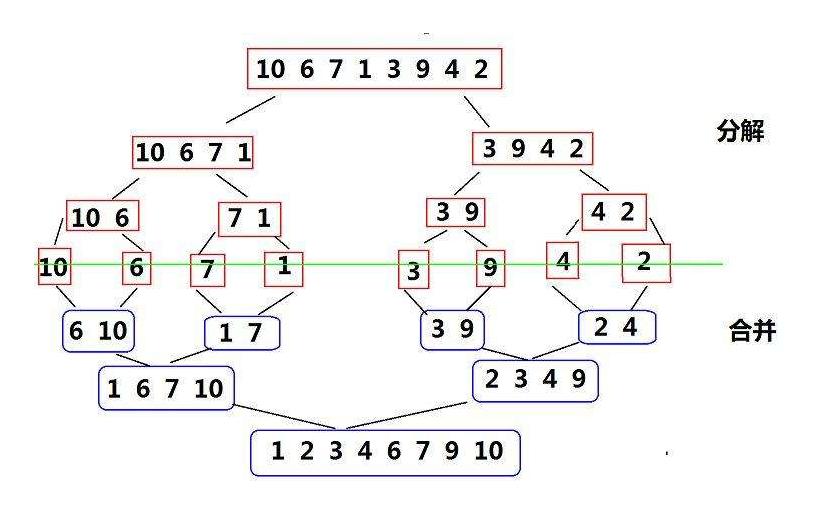
6 归并排序
vector<int> merge(vector<int> left, vector<int> right) {
vector<int> res;
int i = 0, j = 0;
while (i < left.size() && j < right.size()) {
if (left[i] <= right[j])
res.push_back(left[i++]);
else
res.push_back(right[j++]);
}
if (i == left.size())
res.insert(res.end(), right.begin() + j, right.end());
else if (j == right.size())
res.insert(res.end(), left.begin() + i, left.end());
return res;
}
vector<int> mergeSort(vector<int>& arr) {
if (arr.size() < 2) return arr;
int mid = arr.size() / 2;
vector<int> left(arr.begin(), arr.begin() + mid);
vector<int> right(arr.begin() + mid, arr.end());
return merge(mergeSort(left), mergeSort(right));
}
#include "vector"
using namespace std;
void print(vector<int> &nums) {
for (int i = 0; i < nums.size(); ++i) {
printf("%d ", nums[i]);
}
printf("\n");
}
int main() {
vector<int> num = {3, 1, 5, 8, 6, 2, 0, 9, 4, 7};
print(num);
//quicksort(num, 0, 9);
//selectsort(num);
//bubblesort(num);
//insertsort(num);
//heap_sort(num, 10);
vector<int> b = mergeSort(num);
print(b);
return 0;
}
| 排序算法 | 平均时间复杂度 | 最坏时间复杂度 | 最好时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡排序 | O(n²) | O(n²) | O(n) | O(1) | 稳定 |
| 选择排序 | O(n²) | O(n²) | O(n) | O(1) | 不稳定 |
| 插入排序 | O(n²) | O(n²) | O(n) | O(1) | 稳定 |
| 快速排序 | O(nlogn) | O(n²) | O(nlogn) | O(nlogn) | 不稳定 |
| 堆排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(1) | 不稳定 |
| 希尔排序 | O(nlogn) | O(ns) | O(n) | O(1) | 不稳定 |
| 归并排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(n) | 稳定 |
| 计数排序 | O(n+k) | O(n+k) | O(n+k) | O(n+k) | 稳定 |
| 基数排序 | O(N*M) | O(N*M) | O(N*M) | O(M) | 稳定 |
一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度 。